Confidence intervals, confidence level and p-values simply explained!
Let’s talk about p-values and confidence intervals! They’re very common statistical terms, and I thought I had a clear understanding of what both are, but turns out that language can be misleading and often misinterpreted. I thought perhaps some of you might have the same questions as I did when I looked into this topic, so here’s a post about it.
Let’s put ourselves to the test with this example.
‘Rare Pickle Disease is a very rare disease has a median survival of 2 years. In the latest clinical study, drug A was found to have a two-fold increase in survival compared to the control group (p < 0.01, 95% CI 1.5-2.5)‘.
- There’s 5% chance that drug A actually has no effect.
- There’s 1% chance that drug A actually has no effect.
- There’s 95% chance that drug A actually increases the survival between 1.5 and 2.5 years.
Can you tell which statements above are true or false?
Take a guess, if you are not sure.
The answer is… none of the statements above are true. If you are not sure why, hopefully this post will clear things up.
In this post, we will discuss how to interpret p-values and confidence intervals. I will explain both concepts without getting into the maths of it and focusing on understanding the concept behind these statistical terms.
So if you are ready… let’s dive in!
Let’s start with an example…
It’s always easier to understand something applying it to a specific example. But don’t worry, if you are someone who likes definitions, that will come later. Let’s take a look at an example to get a feeling of what p-values and confidence intervals are.
Imagine we want to find out if the mean length of all giant squids in the Atlantic Ocean is larger in males or females.
In other words (statistical words):
H0 (null hypothesis): there are no significant difference between female and male average lengths. Or average length males – average length females = 0.
H1 (alternative hypothesis): there is a significant difference between female and male average lengths. Or average length males – average length females != 0.
So now it’s time to get out there and go fishin’!
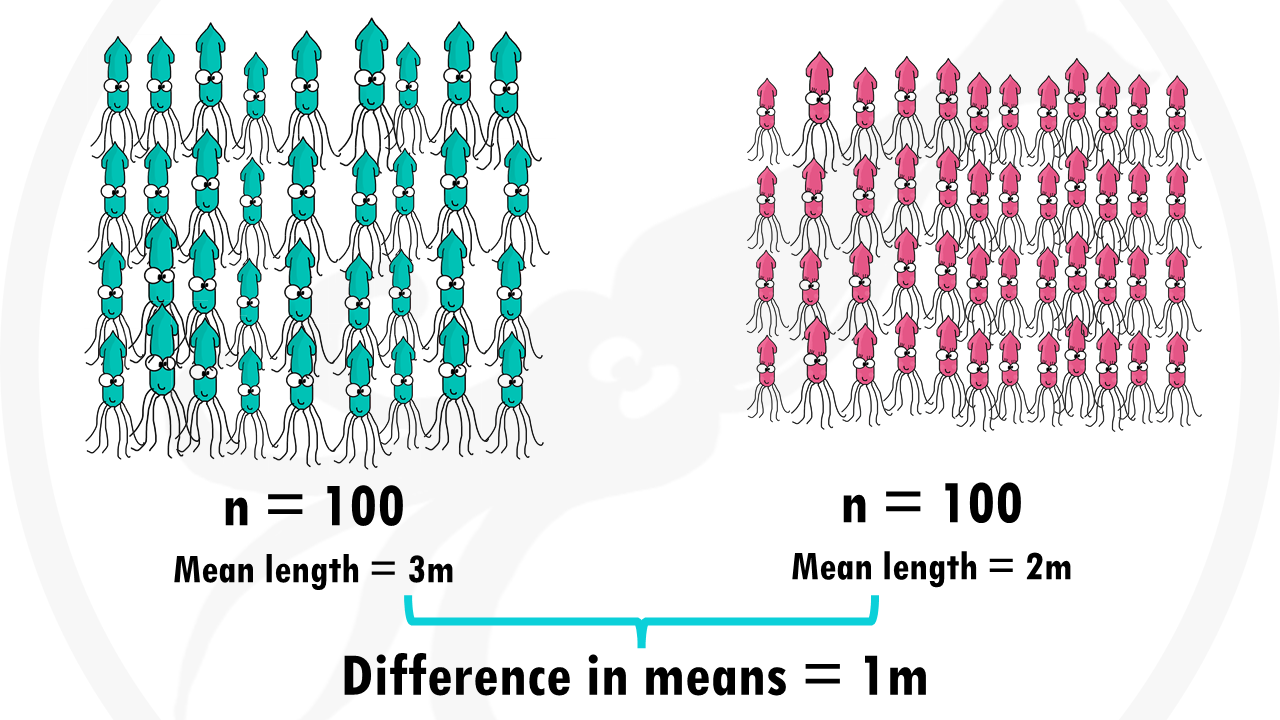
Instead of fishing every single giant squid in the Atlantic Ocean to measure its length (and then return it back to the sea), we select a sample of 100 female squids and 100 male squids.
The mean length of males is 3m. The mean length of females is 2m. What we are actually testing, though, is the difference in means. Based on our sample data, we obtain a 95% confidence interval between 0.5 m and 1.7 m, and a p-value of 0.02.
In summary,
- p-value = 0.02
- CI (confidence interval) = [0.5, 1.7]
- CL (confidence level) = 95%
We decide to go with a p-value threshold of 0.05. That is, since our p-val < 0.05, our results are significant. We can accept the alternative hypothesis (yes, there are significant differences between the averages), and reject the null hypothesis.
Wohoo!
So… what does this actually mean?
What are p-values?
For those of you who like definitions:
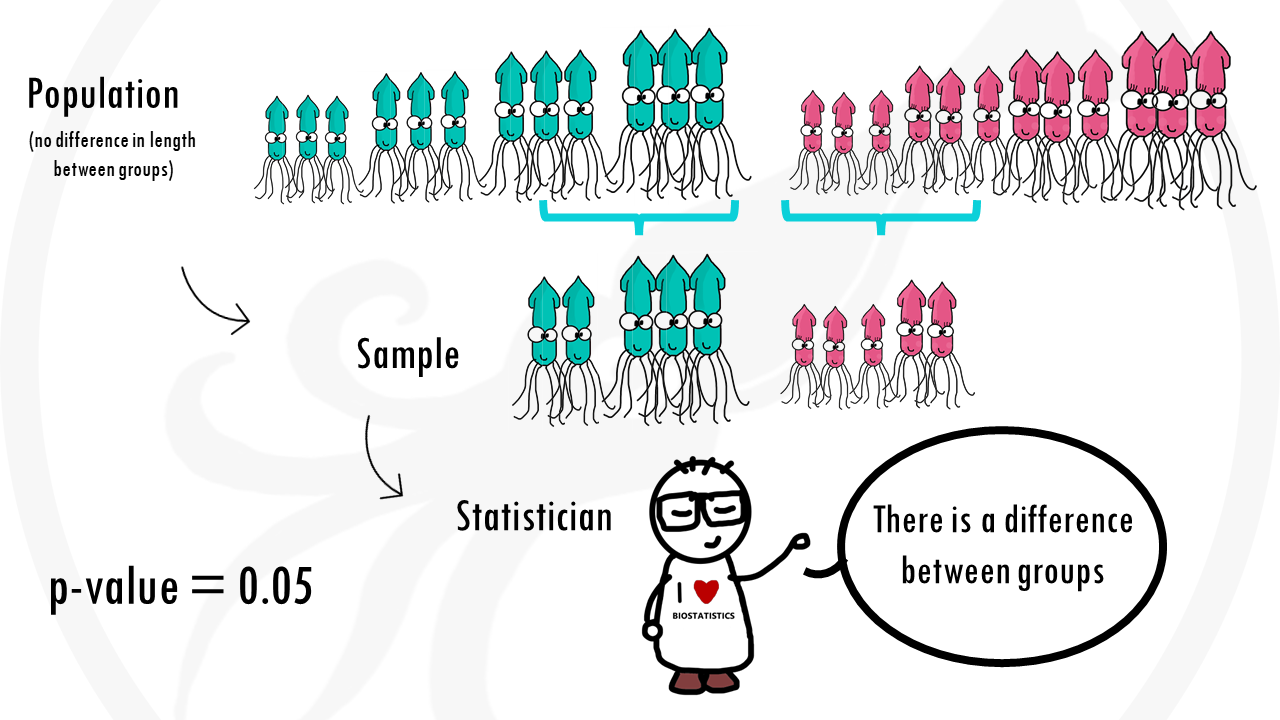
A p-value is the probability of obtaining the result you got—or an even more extreme one—if the null hypothesis is correct.
Applying it to our example, with our data, there is a 2% chance (p-val = 0.02) that we get a difference in average lengths of female and male squid of 1m or more, if in fact there is no difference in lengths between groups. In other words, if male and female squids measured the same on average, what are the chances of taking 100 male and 100 female squids, averaging their lengths, subtracting the means, and getting a difference of 1m or more?
The answer is: 2%.
This brings us to the most common misconception of p-values. Read the following statement carefully, and decide if it is true or false:
With a p-value threshold of 5%, we are accepting that there is a 5% probability that there actually is no significant difference between groups.
The truth is… it is FALSE!
Let’s go back to the definition of p-value. The p-value is the probability of obtaining the result you got—or an even more extreme one—if the null hypothesis is correct. In other words, it is the probability of getting a 1m difference in mean lengths – or more – if there actually no differences between groups. With a p-value threshold of 5%, we are accepting a 5% probability of obtaining those results if there are no differences between groups. In other words, that we were just ‘lucky’ (or unlucky, depends on how you want to see it) – the data we collected had really long male squids and really short female squids but actually in the population there are no differences.
The ‘trick’ here is that the p-value does not tell you if H0 is correct or incorrect. It just tells you how probable it is that you got the results you got, if H0 were correct. The smaller the p-value, the more improbable it is that you got those results if H0 were correct, in other words. Often we take a ‘shortcut’ and say ‘p < 0.05 – we reject the null hypothesis and assume there’s a 5% chance that it is actually correct’. But this is wrong, because the p-value does not inform whether H0 is correct or incorrect, it informs about the probability of obtaining those results from our sample, if H0 were true.
In summary, a p-value tells us how likely we are to have found a particular set of observations (in this case, 200 squid with a difference in length of 1m between males and females) if the null hypothesis were true. The smaller the p-value, the less plausible is the null hypothesis that there is no difference between the groups.
Squidtip
- The p-value is NOT the probability that the null hypothesis is true, or the probability that the alternative hypothesis is false.
- The p-value is not the probability that the observed effects were produced by random chance alone.
- The p-value is the probability of obtaining the result you got—or an even more extreme one—if the null hypothesis is correct.
What about confidence intervals (CI)?
p-values give us the probability of the difference we observed between female and male squids occurring by random chance if in fact, there are no differences. The p-value however does not provide an estimate of what that difference in length means is.
For that we need the confidence interval (CI).
The confidence interval is a range of values calculated by statistical methods which includes the desired true parameter (for example, the arithmetic mean, the difference between two means, the odds ratio…) with a probability defined in advance (coverage probability, confidence probability, or confidence level). The confidence level of 95% is usually selected.
Let’s have a look at what a confidence interval actually means.
Remember we are trying to estimate the difference in mean length between male and female squid. We will never know the actual difference in mean length between male and female squid. It could be 1m, it could be 2m. The true population parameter will always be unknown, because we cannot measure every individual (squid) in the population. The best we can do is estimate it by taking a sample. And the CI tells us how precise our estimate is. A narrower CI means a more precise estimate, a wider CI indicates a less precise estimate.
Let’s try again. True or false?
- If we took another sample of 200 squid and calculated the difference in means, there’s 95% chance the sample would be between 0.5 and 1.7 m.
- About 95% of measurements (in this case, the difference in means) were between 0.5 and 1.7 m.
- We’re 95% confident that the interval (0.5, 1.7) captures the true difference in means.
Try to figure it out based on the definition above.

Ready to find out? The correct answer is that only the last statement is true.
Indeed, we can be 95% sure that the actual difference in means in the population will be between 0.5 and 1.7m.
The CI, however, does NOT make estimates about upcoming values of sample statistics – it just gives us plausible estimates for population parameters. What does this mean? We can only say we’re 95% confident that the interval (0.5, 1.7) captured the true difference in means between female and male lengths. We cannot say anything about the sample itself, the 200 squid we measured.
Actually, just like with any statistic estimated from a sample, the confidence interval will vary from sample to sample.
The first time we went fishing and measured 200 squid, we got a CI between 0.5 and 1.7. If we went fishing again and took another random sample, the CI might be between 1 and 2.2m. If we went fishing a third time, we might get an interval between 0.8 and 2m. If we did this 100 times, we would produce 100 different confidence intervals. Some of the intervals calculated from these random samples will contain the true population parameter, and some will not.
A 95% confidence level means that 95 out of those 100 confidence intervals will contain the true population parameter. Five out of 100 times the actual difference of means in length would be outside the range specified by the CI. And again, we will never know which CIs contain the actual difference in means of the population of squids.
In summary:
- Ideally, we would measure every single giant squid in the Atlantic Ocean, to find the true difference in means between males and females. But we cannot do that. We don’t have a big enough boat.
- The alternative is to take a random sample, like we did, of 100 females and 100 males. This way, we can estimate the difference in means.
- The confidence level (95%) is the probability (or certainty, how sure you are of that result) that the CI contains the true population parameter when you draw a random sample many times.

Squidtip
What do confidence intervals tell us about statistical significance?
If the confidence interval does not include the value of zero effect, it can be assumed that there is a statistically significant result.
In our example, we are 95% sure that the actual difference in mean length between male and female squids is between 0.5m and 1.7m. There’s a 5% chance that the true, actual, population difference in lengths is not in that range. What we’re trying to figure out is whether the value 0 m is within the 95% confidence interval (= not significant) or outside it (= significant).
If we look at it the other way, what if the actual population difference in mean lengths is 0m? So there are no differences. If we got a CI of (-1, 1), then we are 95% sure that the true difference in mean lengths is between -1m and 1m… also 0! So our results are not really informative, we cannot reject H0.
What makes wider or narrower confidence intervals?
The size of the confidence interval depends on the sample size, the standard deviation of groups, and the chosen confidence level.
- Bigger sample size, smaller CI. If the sample size is large, this leads to “more confidence” and a narrower confidence interval. If the confidence interval is wide, this may mean that the sample is small. Think of it this way: if instead of 100, you measured 1000 squid in one go, you would probably be able to say that the difference in means is between 0.8 and 1.2m. If we measure 100,000 squid, we would probably be able to say that the difference in length means is between 0.9 and 1.1m… As the sample size gets closer to the population size, the lower and upper limits of our estimate (the confidence interval) get closer to the actual value.
- Higher standard deviation, wider CI. If the dispersion is high, the conclusion is less certain and the confidence interval becomes wider. If male squids had lengths between 0.5 and 12m, the mean male length would also change more depending on the squids you sample, and your CI would be wider. If male squids are always between 10.5 and 10.6 m long, then you would be more sure of the difference in means.
- Finally, the size of the confidence interval is influenced by the selected level of confidence. A 99% confidence interval is wider than a 95% confidence interval. In general, if you want a higher probability to cover the true value in your range, then the range (the confidence interval) becomes wider.
Boring definitions to sum it all up
p-value – probability that the observed result (difference between the groups being compared)—or one that is more extreme—would occur by random chance, assuming that the null hypothesis (the alternative scenario to the study’s hypothesis) is that there are no differences between the groups being compared.
Confidence Interval (CI)- A range that a measurement or statistical parameter is likely to lie within, given a certain probability. A CI is usually reported as x ± CI or CI(x,y). Note that a CI is meaningless without an idea of how likely the value will fall in that range, a confidence level.
Confidence Level (CL) – The probability that a measurement or statistical parameter exists within the confidence interval. Usually reported with the CI: x ± CI (CL% Confidence Level) or CL% CI x-y
Want to know more?
If you would like to know more about common misconceptions about p-values, check out:
- A Dirty Dozen: Twelve P -Value Misconceptions: dig in deeper into p-value misconceptions with this article.
- The clinician’s guide to p values, confidence intervals, and magnitude of effects: short Nature paper on p-values and confidence intervals.
- Confidence intervals: Correct and incorrect interpretations: nice, easy 5 min read about confidence intervals with an example.
- Confidence Interval or P-Values? Article on the meaning and interpretation of these two statistical concepts.
You can also check out some of my other posts:
- Multiple testing: p-values, q-values and FDR!
- How to interpret a volcano plot
- Correlation and the correlation coefficient.
Ending notes
Wohoo! You made it ’til the end!
In this post, I shared some insights on the meaning and interpretation of p-values and confidence intervals.
Hopefully you found some of my notes and resources useful! Don’t hesitate to leave a comment if there is anything unclear, that you would like explained differently/ further, or if you’re looking for more resources on biostatistics! Your feedback is really appreciated and it helps me create more useful content:)
Before you go, you might want to check:
Squidtastic!
You made it till the end! Hope you found this post useful.
If you have any questions, or if there are any more topics you would like to see here, leave me a comment down below.
Otherwise, have a very nice day and… see you in the next one!
Squids don't care much for coffee,
but Laura loves a hot cup in the morning!

If you like my content, you might consider buying me a coffee.
You can also leave a comment or a 'like' in my posts or Youtube channel, knowing that they're helpful really motivates me to keep going:)
Cheers and have a 'squidtastic' day!
And that is the end of this tutorial!
In this post, I explained the differences between log2FC and p-value, and why in differential gene expression analysis we don't always get both high log2FC and low p-value. Hope you found it useful!
Before you go, you might want to check:
Squidtastic!
You made it till the end! Hope you found this post useful.
If you have any questions, or if there are any more topics you would like to see here, leave me a comment down below.
Otherwise, have a very nice day and... see you in the next one!
