When working with biological data, we often want to compare measurements across multiple groups. However, these measurements aren’t always normally distributed. In such cases, non-parametric methods like the Kruskal-Wallis test and Dunn’s post-hoc test are ideal alternatives to ANOVA.
The Kruskal-Wallis test (H test) is a non-parametric statistical test used to compare three or more independent groups to determine if there are statistically significant differences between them. It is an extension of the Mann-Whitney U test, which is used for comparing two groups.
In this post, we will cover:
- what is the Kruskal-Wallis and Dunn’s test, easily explained with an example
- requirements and when to use this test
- Kruskal-Wallis and Dunn’s test easy tutorial in R
So if you are ready… let’s dive in!
How to compare more than 2 groups of interest?
Imagine you’re studying the effect of three different diets on the cholesterol levels of lab rats:
-
Group 1: Standard lab diet
-
Group 2: High-fat diet
-
Group 3: High-fiber diet
Cholesterol levels don’t follow a normal distribution (verified using Shapiro-Wilk test). So, instead of ANOVA, you choose the Kruskal-Wallis test.
If the Kruskal-Wallis test is significant, then you use Dunn’s test to find out which pairs of diets cause different cholesterol levels (e.g., maybe high-fat differs from high-fiber, but not from the standard diet).
Squidtip
The Kruskal-Wallis test is a non-parametric alternative to one-way ANOVA. It’s used to determine if there are statistically significant differences between the medians of three or more independent groups. However, it only tells you that at least one group is different—it doesn’t specify which groups differ. To determine which specific groups differ after a significant Kruskal-Wallis result, you can use Dunn’s test as a post-hoc analysis.
When to Use the Kruskal-Wallis and Dunn’s Test
You use the Kruskal-Wallis test when:
-
You want to compare three or more independent groups. The test is used for comparing independent groups, meaning the observations in each group are not related.
-
Your data is not normally distributed, or you’re dealing with ordinal data (e.g., ranks or scores). The Kruskal-Wallis test is non-parametric, meaning that, unlike ANOVA, it does not assume a normal distribution of the data, making it suitable for non-normally distributed data.
-
You’re testing if at least one group has a significantly different median value. You won’t know which one is different though! For that, we need the Dunn’s test.
The Dunn’s test is a post-hoc test:
-
Used only after the Kruskal-Wallis test shows a significant difference.
-
It performs pairwise comparisons between groups to see which specific groups differ.
Squidtip
The Kruskal-Wallis test in a nutshell:
- Non-parametric: it is suitable for non-normally distributed data.
- Ordinal or Continuous Data: it can be used with ordinal data or continuous data that has been converted to ranks.
- Independent Groups: used for comparing independent groups, meaning the observations in each group are not related.
Kruskal-Wallis and Dunn’s test in R
Let’s compare the body mass of different penguin species using the palmerpenguins dataset. We’ll walk through how to:
-
Perform a Kruskal-Wallis test,
-
Conduct pairwise post-hoc comparisons using Dunn’s test,
-
Visualize the results using a boxplot with significance annotations.
As always, you can find the entire script in Biostatsquid’s Github page.
# ----------------------
# Kruskal-Wallis & Dunn’s Test on Penguin Data
# ----------------------
# We’ll analyze penguin body mass across different species.
# Setting up environment ===================================================
# Clean environment
rm(list = ls(all.names = TRUE)) # will clear all objects including hidden objects
gc() # free up memory and report the memory usage
options(max.print = .Machine$integer.max, scipen = 999, stringsAsFactors = F, dplyr.summarise.inform = F) # avoid truncated output in R console and scientific notation
# Set seed
set.seed(123456)
# Loading relevant libraries
library(palmerpenguins)
library(FSA)
library(ggplot2)
library(dplyr)
library(ggpubr)
library(rstatix)We begin by loading the palmerpenguins dataset and filtering out rows with missing values for body mass and species. This ensures our analysis runs without errors.
# Load and clean data
data("penguins")
penguins_clean <- penguins %>%
filter(!is.na(body_mass_g), !is.na(species))
# View summary
summary(penguins_clean$species)We’ll use the Kruskal-Wallis test to determine whether there’s a statistically significant difference in median body mass between the penguin species. It’s a non-parametric alternative to one-way ANOVA and is suitable for data that are not normally distributed.
# Kruskal-Wallis test
kruskal_test <- penguins_clean %>%
kruskal_test(body_mass_g ~ species)
print(kruskal_test)> print(kruskal_test)
# A tibble: 1 × 6
.y. n statistic df p method
* <chr> <int> <dbl> <int> <dbl> <chr>
1 body_mass_g 342 218. 2 5.61e-48 Kruskal-WallisEasy! We see that the p-value is significant (p < 0.01). This means there is a statistical difference between at least 2 of the groups. If the Kruskal-Wallis test is significant, we perform Dunn’s test to identify which pairs of species differ. We apply a Bonferroni correction to adjust for multiple comparisons.
# Dunn’s Test (Post-hoc)
dunn_results <- penguins_clean %>%
dunn_test(body_mass_g ~ species, p.adjust.method = "bonferroni")
# This shows pairwise comparisons between species (e.g., Adelie vs Gentoo).Great! We’ve compared body mass between 3 different species of penguin and found significant differences between Adelie & Gentoo, and Chinstrap & Gentoo. There were no significant differences in body mass between Adelie & Chinstrap.
Now, it’s time to plot our results! A great way to visualise these comparisons is with boxplots.
We’ll first add a few extra steps to customise how we display the p-values – the main results of our test. For Kruskal-Wallis, we extract the p-value and, if it’s less than 0.01, we will display "Kruskal-Wallis p < 0.01" at the top of the plot. Otherwise, we show the actual p-value (this is of course, personal preference! You might want to display the entire value).
For Dunn’s test pairwise comparison results, only the comparisons with adjusted p-values below 0.05 are retained and labeled with conventional significance codes:
# Get only significant comparisons
sig_comparisons <- dunn_results %>%
filter(p.adj < 0.05) %>%
select(group1, group2, p.adj) %>%
mutate(p.adj = case_when(
p.adj < 0.001 ~ "***",
p.adj < 0.01 ~ "**",
p.adj < 0.05 ~ "*"
))
# Convert to list of pairs:
comparisons_list <- sig_comparisons %>%
select(group1, group2) %>%
as.list() %>%
t()
# Check p-value
kw_p <- kruskal_test$p
# Create label based on significance
kw_label <- if (kw_p < 0.01) {
"Kruskal-Wallis p < 0.01"
} else {
paste0("Kruskal-Wallis p = ", signif(kw_p, 3))
}
Perfect, now we’re ready for our boxplots! There’s a lot of extra lines of code here to customise the plot and make it pretty, but the main ones are geom_boxplot() for the boxplot themselves, the annotate function (for Kruskal-Wallis result) and the stat_pvalue_manual for the pairwise comparisons.
ggplot(penguins_clean, aes(x = species, y = body_mass_g)) +
geom_boxplot(aes(fill = species)) +
scale_fill_manual(values = c('lightblue', 'lightpink', 'beige')) +
theme_bw() +
labs(title = "Penguin Body Mass by Species",
y = "Body Mass (g)",
x = "") +
theme(legend.position = "none",
axis.text = element_text(size = 14),
axis.title = element_text(size = 16, face = 'bold')
) +
annotate("text", x = 1, y = 6700, label = kw_label, size = 5) +
stat_pvalue_manual(sig_comparisons,
label = "p.adj",
y.position = seq(6200, 6600, length.out = nrow(sig_comparisons)),
tip.length = 0.01)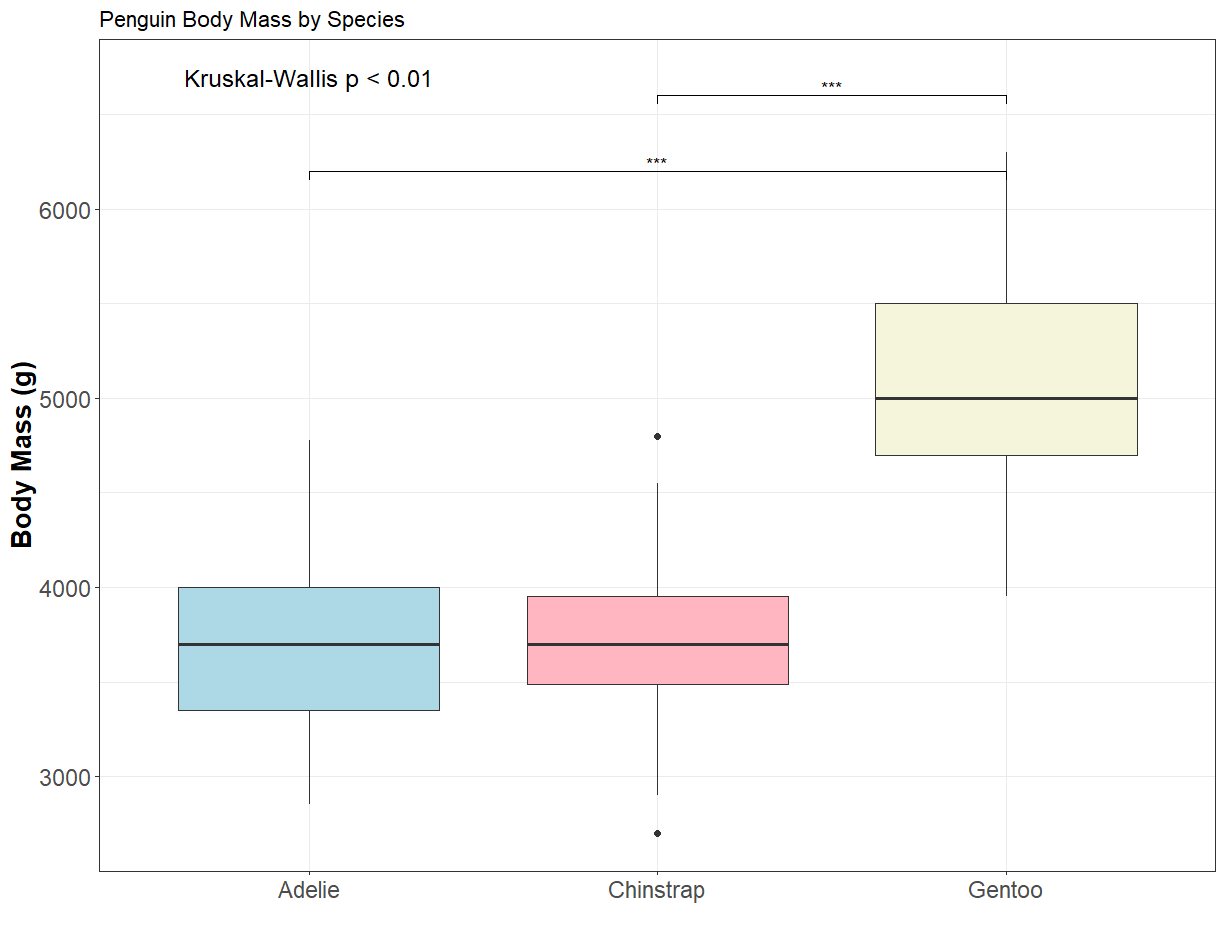
This plot highlights both the overall and pairwise statistical differences in penguin body mass. Nice!
And that is the end of this tutorial!
In this post, we covered the Kruskal-Wallis test for multiple group comparisons. Hope you found it useful!
Before you go, you might want to check:
Squidtastic!
You made it till the end! Hope you found this post useful.
If you have any questions, or if there are any more topics you would like to see here, leave me a comment down below.
Otherwise, have a very nice day and… see you in the next one!